Scalar Inferencing, Polarity and Cognitive Load
Skip to main content
eScholarship
Open Access Publications from the University of California
Refine Search

Glossa Psycholinguistics

Glossa Psycholinguistics banner

Scalar Inferencing, Polarity and Cognitive Load

Published Web Location

https://doi.org/10.5070/G60112566
The data associated with this publication are within the manuscript.
Creative Commons 'BY' version 4.0 license
Abstract

According to the Polarity Hypothesis, the presence or absence of a processing cost for Scalar Inferences (SIs) depends on their polarity. This hypothesis predicts, among other things, that the processing of lower-bounding SIs should not be affected by cognitive load the same way upper-bounding SIs are. To date, evidence in support of this prediction comes from the comparison between upper-bounding and lower-bounding SIs elicited by disparate scalar words. In this paper, we report on two dual-task experiments testing this prediction in a more controlled way by comparing upper-bounding and lower-bounding SIs arising from the same scalar words or scale-mates operating over the same dimension. Results show that, for these more minimal comparisons, lower-bounding SIs involve comparable cognitive demands as their upper-bounding counterparts. These findings challenge the idea that load effects are consistently modulated by SI polarity and suggest instead that these effects are relatively consistent across different types of SIs.

 

Main Content

1 Introduction

An utterance of (1-a) commonly conveys the Scalar Inference (SI) in (1-c). On most accounts of SIs, this pragmatic enrichment is assumed to involve the generation and negation of alternatives, that is, sentences which were not uttered, but would have been equally relevant and more informative in the given context (for an overview, see Chemla & Singh, 2014; Gotzner & Romoli, 2022; Sauerland, 2012). In our example, the relevant SI corresponds to the negation of the alternative to (1-a) in (1-b), where the weak scalar word some has been replaced with its stronger scale-mate, all.

    1. (1)
    1. a.
    1. Some of the apples are red.                                                                                  WeakPos
    1.  
    1. b.
    1. All of the apples are red.                                                                                    Alternative
    1.  
    1. c.
    1. ↝ Not all the apples are red                                                             Upper-bounding SI

There is concurring experimental evidence that processing the interpretation with SI of a sentence like (1-a) can be cognitively demanding (for response delay effects, see Bott & Noveck, 2004; Bott et al., 2012; Breheny et al., 2006; Chemla & Bott, 2014; Chevallier et al., 2008; Cremers & Chemla, 2014; Huang & Snedeker, 2009; Noveck & Posada, 2003; Tomlinson et al., 2013; for cognitive load effects, see De Neys & Schaeken, 2007; Dieussaert et al., 2011; Marty & Chemla, 2013; Marty et al., 2013). The apparent ‘cost’ of SIs is one of the most replicated effects in truth-value judgement studies and it is often thought to be an important marker of this sort of meaning-strengthening operations. To date, however, there has not been wide consensus as to the source of this extra cognitive cost (for an overview, see Khorsheed et al., 2022; Khorsheed & Gotzner, 2023), especially as it is absent from the comprehension and evaluation of semantically equivalent sentences with ‘only’ (Bott et al., 2012; Marty & Chemla, 2013).

A promising account has recently emerged. Investigating whether the response delay and cognitive load effects observed for some generalise to other scalars, van Tiel, Pankratz, and Sun (2019) tested the processing of 7 scalar words differing, inter alia, in their scalarity. Their studies included 5 positive scalars with a literal lower-bound meaning (i.e., some, most, or, might and try), giving rise to upper-bounding SIs (e.g., ‘some of the food’ implicates ‘not all of the food’), and 2 negative scalars with a literal upper-bound meaning (i.e., scarce and low), giving rise to lower-bounding SIs (e.g., ‘low on food’ implicates ‘some food’). Their results show that, while all scalars from the first category displayed the classical effects, neither of those from the second category did (see also van Tiel, Marty, Pankratz, & Sun, 2019; van Tiel & Pankratz, 2021). The authors explain these findings by hypothesising that only upper-bounding SIs are cognitively demanding and that the extra processing cost they incur stems from the fact that, unlike lower-bounding SIs, these SIs introduce negative propositions into the meaning of the sentence, the processing of which is independently known to be cognitively effortful (a.o., Clark & Chase, 1972; Geurts et al., 2010; Deschamps et al., 2015). This hypothesis, dubbed the Polarity Hypothesis (van Tiel & Pankratz, 2021; also referred to as the Scalarity hypothesis in van Tiel, Pankratz, & Sun, 2019; van Tiel, Marty, Pankratz, and Sun, 2019), is stated in (2). The polarity-based explanation departs from the former explanation in Marty et al. (2013) where the extra cognitive cost associated with SI interpretations is linked to ambiguity resolution and located in the processing stage involving the decision to derive or not the SI (see Gotzner, 2019 for a similar proposal).

    1. (2)
    1. Polarity Hypothesis
    2. SIs are cognitively demanding insofar as they introduce an upper-bound on the dimension over which the scalar word quantifies.

As van Tiel, Pankratz, and Sun (2019) acknowledge, however, the scalar words in their sample differ in more respects than just the polarity of the SI they can give rise to, such as the type of dimension over which they quantify or the parts of speech they come from (e.g., only the negative scalars were adjectival). In the absence of more minimal comparisons, van Tiel et al.’s results leave open the possibility that the contrasts they observed reflect idiosyncrasies of the negative scalars they tested, rather than a general difference in the processing signature of upper-bounding and lower-bounding SIs.1

In this paper, we focus on the cognitive load effects associated with the derivation of SIs and offer a direct test of the predictions of the Polarity Hypothesis by comparing the upper-bounding and lower-bounding SIs arising (i) from the same scalars and (ii) from different scalars belonging to the same scale. Crucially, these SIs differ in terms of polarity but otherwise involve the same words and concepts, e.g., ‘some’ implicates not all while ‘some not’ and ‘not all’ implicate some. Our results demonstrate that, for such comparisons, lower-bounding SIs involve comparable cognitive demands as their upper-bounding counterparts.

2 Experiments

We conducted two experiments, both based on the same method and procedure as in van Tiel, Pankratz, and Sun (2019, Experiment 2). In both experiments, participants had to perform a sentence-picture verification task. In the target conditions, sentences were presented with a picture that made them false if the relevant SI is derived, but true otherwise. Participant’s cognitive resources during sentence verification were experimentally burdened by adding a secondary memory task and by modulating further the complexity of the visual pattens to be memorised (see also De Neys & Schaeken, 2007; Marty & Chemla, 2013; van Tiel, Marty, et al., 2019). If the derivation of a given SI requires additional processing resources, then that SI should become less available under higher cognitive load, i.e., in situations where these resources are impaired by the concurrent memory task, resulting in higher acceptance rates in the target conditions.

Experiment 1 tested WeakPos sentences like (1-a), where a weak scalar term appears in a positive sentence, and compared them to their WeakNeg variants, where negation is added below the same scalar term, as in (3-a). The latter give rise to lower-bounding SIs conveying what is literally expressed by their WeakPos counterparts. All theories of SIs explain the SI in (3-c) as arising from the alternative in (3-b).

    1. (3)
    1. a.
    1. Some of the apples are not red.                                                                            WeakNeg
    1.  
    1. b.
    1. All of the apples are not red.                                                                              Alternative
    1.  
    1. c.
    1. ↝ Some of the apples are red                                                           Lower-bounding SI

Experiment 2 tested the same WeakPos sentences as in Experiment 1, but compared them to their NegStrong variants, where the stronger scale-mate of the weaker term is embedded under negation, as in (4). The latter give rise to the same lower-bounding SIs as the WeakNeg sentences above. All theories of SIs explain the SI in (4-c) as arising from the alternative in (4-b).

    1. (4)
    1. a.
    1. Not all of the apples are red.                                                                            NegStrong
    1.  
    1. b.
    1. Not some (=none) of the apples are red.                                                   Alternative
    1.  
    1. c.
    1. ↝ Some of the apples are red                                                          Lower-bounding SI

WeakPos sentences were expected to exhibit the load effects previously reported in the literature. Their negative variants provided us with novel and more minimal comparison points for testing the predictions of the Polarity Hypothesis. If the relevant effects are specific to upper-bounding SIs, responses to WeakNeg and NegStrong sentences should be left unaffected by our manipulation of the cognitive load; consequently, these sentences should pattern distinctly from their WeakPos counterparts across load conditions.

2.1 Participants

For each experiment, 150 participants were recruited online through Prolific (first language: English; country of residence: UK, USA; minimum prior approval rate: 90%) and paid for their participation (£9.5/hr).

2.2 Design and Materials

Building upon the materials and method in van Tiel, Pankratz, and Sun (2019), we constructed, for each experiment, three tasks that manipulated the cognitive load on participants’ executive resources during sentence comprehension: one sentence-picture verification task (NoLoad), and two dual-tasks in which participants had to perform that verification task while trying to remember either a simple square pattern (LowLoad) or a more complex one (HighLoad), as exemplified in Figure 1. Each participant in our studies only ever completed one of these tasks.

Figure 1
Figure 1

Examples of (a) low-load and (b) high-load patterns used in Exp 1 and Exp 2.

The verification task tested three scales: ⟨some, all⟩, ⟨or, and⟩ and ⟨possible, certain⟩. For each scale, we constructed one positive sentence with the weaker term (WeakPos), one negative sentence where negation takes scope below the weaker term (WeakNeg), and one negative sentence where negation takes scope above the stronger term (NegStrong). Each sentence was paired with three types of pictures depicting a situation in which it was unambiguously true (True), unambiguously false (False), or in which its truth-value depended on whether the relevant SI was computed (Target). Both Exp 1 and Exp 2 tested WeakPos sentences along with one of their negative variants, WeakNeg in Exp 1 and NegStrong in Exp 2. Figure 2 shows example sentences and pictures for each scale.2

Figure 2
Figure 2

Sentences and example displays for each scale tested in Exp 1 and Exp 2.

Crossing sentence and picture types gave rise, in each experiment, to 18 conditions (3 scales × 2 sentence types × 3 picture types), each of which was instantiated 3 times by varying the contents of the pictures, resulting in 54 test trials. Following the suggestion in Marty and Chemla (2013), we added in both experiments 3 true and 3 false instances of the only-variants to the WeakPos some-sentences (e.g., Only some of the socks are pink) to serve as additional controls. The mean acceptance rate for these sentences was above 97.5% in their true conditions and below 11.5% in their false conditions in all three tasks of both experiments. These results are in line with the findings from Marty and Chemla (2013) in showing that the interpretation of only-sentences was largely unaffected by load manipulations. These items can be thus set aside in the following.

2.3 Procedure

Participants were pseudo-randomly assigned one of the three tasks so as to reach a balanced number of subjects per task. They were presented with the instructions corresponding to the relevant task and were given one example trial. Each survey started with 4 unannounced practice trials and then continued with the test trials, presented in random order. In the NoLoad task, each trial consisted of the presentation of a sentence-picture item. Participants had to decide whether or not the sentence was a good description of the depicted situation by pressing one of two response keys on their keyboard. In the LowLoad and HighLoad tasks, each trial started with the brief presentation of a pattern of squares (1200 ms for low-load patterns and 1500 ms for high-load patterns). Afterwards, a sentence-picture item was displayed on the screen, exactly as in the NoLoad task. Once participants had entered their answer, they were presented with an empty matrix and asked to recreate the pattern of squares presented at the start of the trial. Participants could fill or unfill squares in the matrix by clicking on them.

2.4 Data treatment

4 participants in Exp 1 and 5 participants in Exp 2 were excluded either for failing to complete the whole survey or for making mistakes in more than 25% of the control sentence-picture items. The mean accuracy rate on control items of the remaining participants was above 93% across all load conditions in both experiments, indicating that these participants had no problem judging the test sentences in their True and False conditions, even under high cognitive load. The mean number of correctly localised squares was above .92 for the simple 1-square patterns and above 2.85 for the complex 4-square patterns in both experiments, indicating that participants performed the memory tasks appropriately.

2.5 Data analysis

To analyse the effects of cognitive load and determine whether they differ across upper-bounding and lower-bounding SIs, we fitted a Bayesian mixed effects logistic regression model to the results of the experiments using the brms package (Bürkner, 2017, 2018, 2021) in R version 4.1.2 (R Core Team, 2021). The model predicted responses in the target conditions on the basis of three categorical predictors, each with three levels – Polarity (WeakPos, WeakNeg, NegStrong), Load (No, Low, High) and Scale (⟨some, all⟩, ⟨or, and⟩ and ⟨possible, certain⟩) – and the interactions among them. These predictor variables were all sum-coded. The mixed effects structure of the model consisted of by-item random intercepts and by-participant random intercepts and slopes for Polarity and Scale, and their interactions with all correlations among them.

The priors were weakly informative priors, which we constructed based on the results of van Tiel, Marty, et al. (2019). Their experiment is identical to the ones reported here, except that no linguistic stimuli contained overt negation. We fitted a logistic mixed effect regression model to the data from their target conditions using the glmer function from the lme4 package, which predicted responses on the basis of two sum-coded categorical variables, Load and Scale, and their interaction. The mixed effects were by-item random intercepts and by-participant random intercepts and slopes for Scale and their correlation. We took the estimates βi of this model and used N(βi, 1) as the priors for the respective fixed effect parameters. For the missing fixed effects, all of which have to do with Polarity, we assumed a fairly broad prior distribution N(1, 1). For mixed effects, the standard deviations were all assumed to come from the Half-Cauchy distribution with σ = 2 and the variance-covariance matrix from the Lewandowski-Kurowicka-Joe distribution with η = 1.3 The posterior distributions reported below were estimated using four Hamilton Monte Carlo Markov Chains implemented in Stan. Each of these chains consisted of 10,000 samples, of which 1,000 were used for warm-up. Both the trace plots (omitted here) and the R̂ values indicated convergence.

2.6 Results

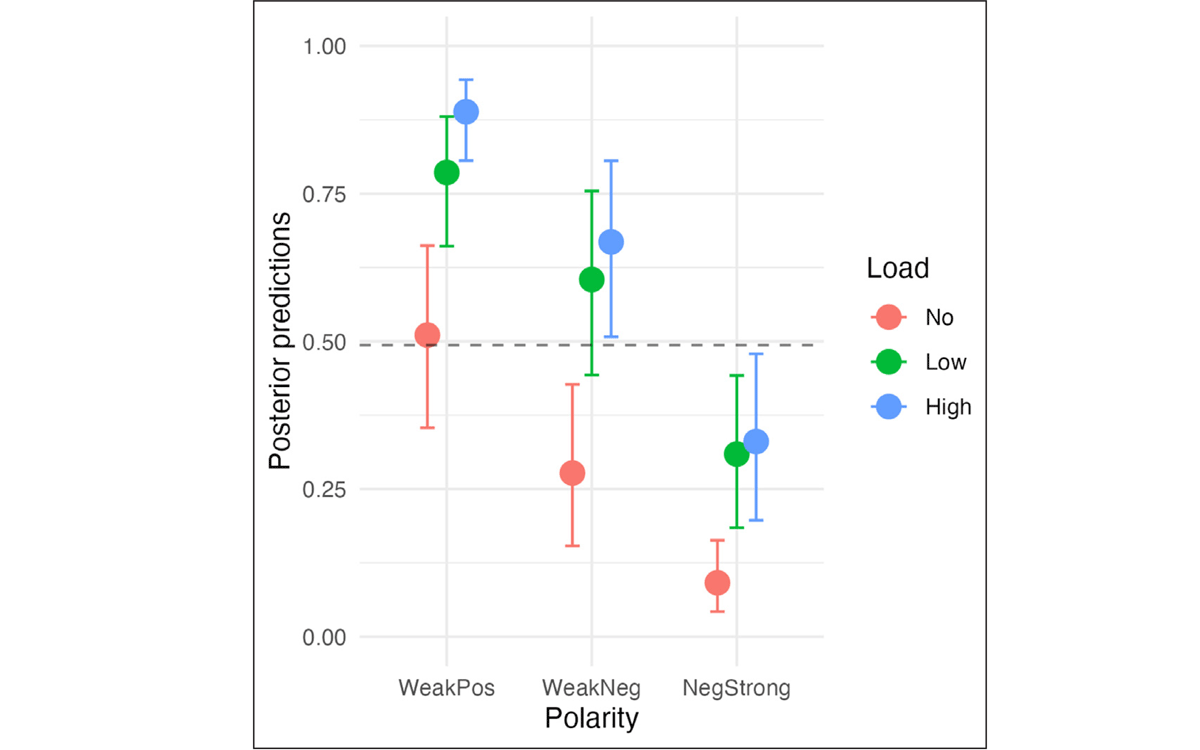
Figure 3 shows the observed mean acceptance rates in the verification task. Overall, results replicate previous findings that people derive fewer upper-bound SIs when their executive cognitive resources are burdened. Responses to the WeakPos sentences were as expected in showing that, in the target conditions, participants accepted these sentences more often under higher cognitive load, both in Exp 1 (No: M = 52, 95% CI [47,57]; Low: M = 58, 95% CI [53,62]; High: M = 69, 95% CI [64,73]) and Exp 2 (No: M = 47, 95% CI [42,51]; Low: M = 65, 95% CI [60,69]; High: M = 68, 95% CI [63,72]).4 Moreover, WeakNeg and NegStrong sentences were found to pattern similarly with their WeakPos counterparts, as shown by the posterior predictions of the Polarity × Load coefficient in Figure 4.

Figure 3
Figure 3

Mean acceptance rates for each scale by sentence type, cognitive load and picture condition in Exp 1 and Exp 2. Error bars represent 95% binomial confidence intervals.

Figure 4
Figure 4

Posterior predictions of the Polarity × Load coefficient. The dotted horizontal line represents the predicted grand mean, and the error bars represent 95% quantiles.

The prediction of the Polarity Hypothesis that Load should affect WeakPos more robustly than the other Polarity levels was tested by determining if, compared to their negative variants, WeakPos sentences gave rise to reliably larger differences between the Low and No conditions (Hypothesis 1), and between the High and No conditions (Hypothesis 2), using the hypothesis() function of brms.5 For the Low-No comparisons, the posterior probabilities of WeakPos having larger differences than WeakNeg and NegStrong were 37% and 32% with evidence ratios of 0.60 and 0.47, respectively, and the differences between the differences were estimated to be –0.13 and –0.24 with 90% quantiles being [–0.82, 0.56] and [–1.11, 0.63]. For the High-No comparisons, the corresponding posterior probabilities were both 80% with evidence ratios of 3.98 and 4.03, respectively, and the differences between the differences were estimated to be 0.37 and 0.45 with 90% quantiles being [–0.34, 1.11] and [–0.42, 1.35]. Thus, our data provides evidence against Hypothesis 1 and weak evidence for Hypothesis 2.

Finally, the same two hypotheses were tested for each level of Scale. The results are summarised in Table 1. Very little variation was found between positive and negative scalar sentences among the three scales regarding the Load effects. Specifically, none of the test cases had notable evidence for Hypothesis 1 and only two of them had notable evidence for Hypothesis 2: the High-No difference for WeakPos was larger than that for WeakNeg with ⟨possible, certain⟩ and larger than that for NegStrong with ⟨or, and⟩. Hence, we conclude there is no across-the-board difference in the effect of Load depending on Polarity.

Table 1

Results of hypothesis testing about the Load effect at different Polarity levels for each Scale.

Scale Hypothesis Estimate 90%CI Evid. Ratio Prob.
⟨some, all⟩ Low–No WeakPos > WeakNeg 0.02 [–1.06, 1.10] 1.03 0.51
WeakPos > NegStrong –0.35 [–1.56, 0.85] 0.45 0.31
High–No WeakPos > WeakNeg –0.15 [–1.27, 0.94] 0.73 0.42
WeakPos > NegStrong 0.68 [–0.53, 1.86] 4.69 0.82
⟨or, and⟩ Low–No WeakPos > WeakNeg –0.12 [–1.04, 0.79] 0.72 0.42
WeakPos > NegStrong –0.48 [–1.62, 0.67] 0.32 0.24
High–No WeakPos > WeakNeg 0.02 [–0.95, 1.00] 1.05 0.51
WeakPos > NegStrong 0.94 [–0.26, 2.11] 9.26 0.90
⟨possible, certain⟩ Low–No WeakPos > WeakNeg –0.30 [–1.41, 0.81] 0.49 0.33
WeakPos > NegStrong 0.11 [–1.47, 1.59] 1.24 0.55
High–No WeakPos > WeakNeg 1.25 [0.09, 2.47] 25.49 0.96
WeakPos > NegStrong –0.25 [–1.83, 1.32] 0.66 0.40

3 Discussion

We tested the predictions of the Polarity Hypothesis by comparing upper-bounding and lower-bounding SIs arising from scalar words operating over the same dimension. Our results reproduce the load effects associated with upper-bounding SIs arising from positive sentences and show that comparable effects extend to the lower-bounding SIs associated with the negative variants of these sentences, whether they involve the same scalars or their stronger scale-mate. We take these results to show that load effects are not specific to upper-bounding SIs and to suggest instead that, for such minimal comparisons, these effects are relatively uniform across different types of SIs. These findings are challenging for the Polarity Hypothesis and for the idea that the polarity of an SI is the only or main explanation of the load effects. On the other hand, they remain compatible with Marty and Chemla (2013)’s proposal that executive cognitive resources are needed to entertain and decide among competing readings and that, when these resources are impaired, speakers default to the more readily accessible interpretation – for scalar sentences, their literal interpretation.

This study leaves us with two open issues. First, it remains to be understood why the SI interpretation of certain negatively scalar words like scarce and low appear to be immune from load effects, as per van Tiel, Pankratz, and Sun (2019)’s results. But we note that this pattern is not unattested: Marty et al. (2013) found a similar pattern with other scalar expressions, specifically numerals. Second, it remains the case that response time results reported so far in the literature largely line up with the Polarity Hypothesis, since the classical response delay effects do not appear to generalise to lower-bounding SIs, whether they arise from negatively scalar words (van Tiel, Pankratz, & Sun, 2019; van Tiel & Pankratz, 2021) or negated scalars (Cremers & Chemla, 2014; Romoli & Schwarz, 2015). This suggests that dual-task and response time results need not pattern together with SIs and, consequently, that both types of measures may reflect distinct cognitive effects (see Marty et al., 2020 for similar suggestions). More work is thus required to evaluate why this disparity emerges.

Data accessibility statement

Data files and analysis scripts associated with the experiments reported in this paper are available open access on the OSF platform at https://osf.io/wrs94/.

Ethics and consent

The experiments were conducted in accordance with the Declaration of Helsinki. Written informed consent was obtained from all participants prior to experimentation, based on a detailed description of the experimental procedure, the reward scheme, and our use of the submitted data. Data were collected and stored in accordance with the provisions of Data Protection Act 2018. The study was approved by the UCL Research Ethics Committee (UCL REC) under approval protocol for non-invasive research on healthy adults LING-2021-01-21.

Funding information

This research was partially supported by the Leverhulme Trust grant RPG-2018-425 awarded to R. Breheny, N. Klinedinst, J. Romoli and Y. Sudo. We also thank the Faculty of Philosophy, Theology and Religious Studies of the Radboud University Nijmegen for additional financial support.

Acknowledgements

We are very grateful to Alan Bale, Matthew Husband, Anna Papafragou, Stephen Politzer-Ahles, audience members at ELM 1 and at the 33rd Annual CUNY Human Sentence Processing Conference as well as to three anonymous reviewers for insightful discussion and useful suggestions.

Competing interests

The authors have no competing interests to declare.

Author contributions

Paul Marty: Conceptualization, Methodology, Resources, Investigation, Formal analysis, Visualization, Writing – original draft, Writing – review & editing

Jacopo Romoli: Conceptualization, Methodology, Writing – review & editing

Yasutada Sudo: Conceptualization, Methodology, Formal analysis, Visualization, Writing – review & editing

Bob van Tiel: Conceptualization, Methodology, Resources, Writing – review & editing

Richard Breheny: Conceptualization, Methodology, Supervision, Writing – review & editing

Author Affiliations

Paul Marty orcid.org/0000-0003-4459-1933

Jacopo Romoli orcid.org/0000-0003-2165-4559

Yasutada Sudo orcid.org/0000-0003-0248-9308

Bob van Tiel orcid.org/0000-0002-4169-3179

Richard Breheny orcid.org/0000-0001-7801-9914

Notes

  1. It should also be noted that the Polarity Hypothesis only offers a partial explanation of previous findings on SI costs. For instance, it does not explain why there is an extra cost to the SI interpretation of ‘some’-sentences compared to the literal interpretation of their ‘only’-variants (Bott et al., 2012; Marty & Chemla, 2013). Similarly, it does not explain the findings in Bott and Frisson (2022) that SI interpretations of ‘some’-sentences are faster to come about when preceded by their canonical ‘all’-alternative. Findings like the above suggest that the cost of (upper-bounding) SIs is not reducible to the processing of negative propositions. [^]
  2. The NegStrong sentence for ⟨or, and⟩ involved a clausal conjunction embedded under a sentence-internal negation (i.e., Not both the apple and the pepper is red). We chose this construction because it was structurally closer to the WeakPos and other NegStrong sentences than other candidates involving external negation (e.g., It is not the case that both the apple and the pepper are red) or nominal conjunction (e.g., The apple and the pepper are not both red). We note, however, that this construction is marked and that its use is felicitous in fewer contexts than the other candidates we just mentioned. The results for these NegStrong conditions should be thus interpreted with caution. [^]
  3. We follow here the recommendations of Gelman (2006), Gelman, Carlin, Stern, and Rubin (2013) and McElreath (2015). In particular, the motivation for using (Half-)Cauchy distributions as priors for variance parameters is that Cauchy distributions have relatively long and even tails, especially compared to normal distributions, which make them good candidates for weakly informative priors. Other commonly used priors for variance parameters include Half-Normal (Schad, Betancourt, & Vasishth, 2021; Vasishth, Yadav, Schad, & Nicenboim, 2023) and Exponential (McElreath, 2020). All the sources cited above recommend Lewandowski-Kurowicka-Joe distributions for weakly informative priors for correlation matrices. [^]
  4. M stands for mean acceptance rate and CI for (binomial proportion) confidence intervals. 95% CIs were calculated from participants’ binary responses using Wilson’s method and transformed into percentages. [^]
  5. Among other things, the hypothesis() function of brms computes an evidence ratio for each hypothesis. For a one-sided hypothesis of the form a > b, as in the present case, the evidence ratio is just the ratio of the posterior probability of a > b and the posterior probability of a < b, that is, the posterior probability under the hypothesis against the posterior probability under its alternative. [^]

References

Bott, L., Bailey, T. M., & Grodner, D. (2012). Distinguishing speed from accuracy in scalar implicatures. Journal of Memory and Language, 66(1), 123–142. DOI:  http://doi.org/10.1016/j.jml.2011.09.005

Bott, L., & Frisson, S. (2022). Salient alternatives facilitate implicatures. PLOS One, 17(3), e0265781. DOI:  http://doi.org/10.1371/journal.pone.0265781

Bott, L., & Noveck, I. A. (2004). Some utterances are underinformative: the onset and time course of scalar inferences. Journal of Memory and Language, 51(3), 437–457. DOI:  http://doi.org/10.1016/j.jml.2004.05.006

Breheny, R., Katsos, N., & Williams, J. (2006). Are generalised scalar implicatures generated by default? An on-line investigation into the role of context in generating pragmatic inferences. Cognition, 100(3), 434–463. DOI:  http://doi.org/10.1016/j.cognition.2005.07.003

Bürkner, P. C. (2017). brms: An R package for Bayesian multilevel models using Stan. Journal of Statistical Software, 80(1), 1–28. DOI:  http://doi.org/10.18637/jss.v080.i01

Bürkner, P. C. (2018). Advanced Bayesian multilevel modeling with the R package brms. The R Journal, 10(1), 395–411. DOI:  http://doi.org/10.32614/RJ-2018-017

Bürkner, P. C. (2021). Bayesian item response modeling in R with brms and Stan. Journal of Statistical Software, 100(5), 1–54. DOI:  http://doi.org/10.18637/jss.v100.i05

Chemla, E., & Bott, L. (2014). Processing inferences at the semantics/pragmatics frontier: disjunctions and free choice. Cognition, 130(3), 380–396. DOI:  http://doi.org/10.1016/j.cognition.2013.11.013

Chemla, E., & Singh, R. (2014). Remarks on the experimental turn in the study of scalar implicature, part I. Language and Linguistics Compass, 8(9), 373–386. DOI:  http://doi.org/10.1111/lnc3.12081

Chevallier, C., Noveck, I. A., Nazir, T., Bott, L., Lanzetti, V., & Sperber, D. (2008). Making disjunctions exclusive. Quarterly Journal of Experimental Psychology, 61(11), 1741–1760. DOI:  http://doi.org/10.1080/17470210701712960

Clark, H. H., & Chase, W. G. (1972). On the process of comparing sentences against pictures. Cognitive Psychology, 3(3), 472–517. DOI:  http://doi.org/10.1016/0010-0285(72)90019-9

Cremers, A., & Chemla, E. (2014). Direct and indirect scalar implicatures share the same processing signature. In Pragmatics, semantics and the case of scalar implicatures (pp. 201–227). Springer. DOI:  http://doi.org/10.1057/9781137333285_8

De Neys, W., & Schaeken, W. (2007). When people are more logical under cognitive load: dual task impact on scalar implicature. Experimental Psychology, 54(2), 128–133. DOI:  http://doi.org/10.1027/1618-3169.54.2.128

Deschamps, I., Agmon, G., Loewenstein, Y., & Grodzinsky, Y. (2015). The processing of polar quantifiers, and numerosity perception. Cognition, 143, 115–128. DOI:  http://doi.org/10.1016/j.cognition.2015.06.006

Dieussaert, K., Verkerk, S., Gillard, E., & Schaeken, W. (2011). Some effort for some: further evidence that scalar implicatures are effortful. Quarterly Journal of Experimental Psychology, 64(12), 2352–2367. DOI:  http://doi.org/10.1080/17470218.2011.588799

Gelman, A. (2006). Prior distributions for variance parameters in hierarchical models (comment on article by Browne and Draper). Bayesian Analysis, 1, 515–534. DOI:  http://doi.org/10.1214/06-BA117A

Gelman, A., Carlin, J., Stern, H., & Rubin, D. (2013). Bayesian data analysis, third edition. Chapman and Hall/CRC Texts in Statistical Science (London: Taylor and Francis). DOI:  http://doi.org/10.1201/b16018

Geurts, B., Katsos, N., Cummins, C., Moons, J., & Noordman, L. (2010). Scalar quantifiers: logic, acquisition, and processing. Language and Cognitive Processes, 25(1), 130–148. DOI:  http://doi.org/10.1080/01690960902955010

Gotzner, N. (2019). The role of focus intonation in implicature computation: a comparison with only and also. Natural Language Semantics, 27(3), 189–226. DOI:  http://doi.org/10.1007/s11050-019-09154-7

Gotzner, N., & Romoli, J. (2022). Meaning and alternatives. Annual Review of Linguistics, 8, 213–234. DOI:  http://doi.org/10.1146/annurev-linguistics-031220-012013

Huang, Y. T., & Snedeker, J. (2009). Online interpretation of scalar quantifiers: insight into the semantics–pragmatics interface. Cognitive Psychology, 58(3), 376–415. DOI:  http://doi.org/10.1016/j.cogpsych.2008.09.001

Khorsheed, A., & Gotzner, N. (2023). A closer look at the sources of variability in scalar implicature derivation: a review. Frontiers in Communication, 8, 1187970. DOI:  http://doi.org/10.3389/fcomm.2023.1187970

Khorsheed, A., Price, J., & van Tiel, B. (2022). Sources of cognitive cost in scalar implicature processing: a review. Frontiers in Communication, 7, 990044. DOI:  http://doi.org/10.3389/fcomm.2022.990044

Marty, P., & Chemla, E. (2013). Scalar implicatures: working memory and a comparison with ‘only’. Frontiers in Psychology, 4, 403. DOI:  http://doi.org/10.3389/fpsyg.2013.00403

Marty, P., Chemla, E., & Spector, B. (2013). Interpreting numerals and scalar items under memory load. Lingua, 133, 152–163. DOI:  http://doi.org/10.1016/j.lingua.2013.03.006

Marty, P., Romoli, J., Sudo, Y., van Tiel, B., & Breheny, R. (2020). Processing implicatures: a comparison between direct and indirect SIs. Paper presented at ELM 1 and at the 33rd Annual CUNY Human Sentence Processing Conference. Retrieved from https://osf.io/5dkfa. DOI:  http://doi.org/10.17605/OSF.IO/AE7PR

McElreath, R. (2015). Statistical rethinking: a Bayesian course with examples in R and Stan, first edition. Chapman and Hall/CRC. Boca Raton.

McElreath, R. (2020). Statistical rethinking: a Bayesian course with examples in R and Stan, second edition. Chapman and Hall/CRC. Boca Raton. DOI:  http://doi.org/10.1201/9780429029608

Noveck, I. A., & Posada, A. (2003). Characterizing the time course of an implicature: an evoked potentials study. Brain and Language, 85(2), 203–210. DOI:  http://doi.org/10.1016/S0093-934X(03)00053-1

R Core Team. (2021). R: A language and environment for statistical computing [Computer software manual]. Vienna, Austria. Retrieved from https://www.R-project.org/

Romoli, J., & Schwarz, F. (2015). An experimental comparison between presuppositions and indirect scalar implicatures. In Experimental perspectives on presuppositions (pp. 215–240). Springer. DOI:  http://doi.org/10.1007/978-3-319-07980-6_10

Sauerland, U. (2012). The computation of scalar implicatures: pragmatic, lexical or grammatical? Language and Linguistics Compass, 6(1), 36–49. DOI:  http://doi.org/10.1002/lnc3.321

Schad, D. J., Betancourt, M., & Vasishth, S. (2021). Toward a principled bayesian workflow in cognitive science. Psychological Methods, 26(1), 103. DOI:  http://doi.org/10.1037/met0000275

Tomlinson, J. M., Bailey, T. M., & Bott, L. (2013). Possibly all of that and then some: scalar implicatures are understood in two steps. Journal of Memory and Language, 69(1), 18–35. DOI:  http://doi.org/10.1016/j.jml.2013.02.003

van Tiel, B., Marty, P., Pankratz, E., & Sun, C. (2019). Scalar inferences and cognitive load. In Proceedings of Sinn und Bedeutung (Vol. 23, pp. 427–442). DOI:  http://doi.org/10.18148/sub/2019.v23i2.622

van Tiel, B., & Pankratz, E. (2021). Adjectival polarity and the processing of scalar inferences. Glossa: a journal of general linguistics, 6(1). DOI:  http://doi.org/10.5334/gjgl.1457

van Tiel, B., Pankratz, E., & Sun, C. (2019). Scales and scalarity: processing scalar inferences. Journal of Memory and Language, 105, 93–107. DOI:  http://doi.org/10.1016/j.jml.2018.12.002

Vasishth, S., Yadav, H., Schad, D. J., & Nicenboim, B. (2023). Sample size determination for Bayesian hierarchical models commonly used in psycholinguistics. Computational Brain & Behavior, 6(1), 102–126. DOI:  http://doi.org/10.1007/s42113-021-00125-y




Top